Fehlermaße: Wie Sie die Güte Ihrer Forecasts auswerten
- Mittlerer absoluter Fehler (MAE)
- Mittlerer absoluter prozentualer Fehler (MAPE)
- Mittlerer quadratischer Fehler (MSE)
- Wurzel des mittleren quadratischen Fehlers (RMSE)
- Wurzel des mittleren quadratischen Fehlers, normalisiert (NRMSE)
- Gewichteter absoluter prozentualer Fehler (WAPE)
- Gewichteter mittlerer absoluter prozentualer Fehler (WMAPE)
- Spannbreite von Fehlern und Ungenauigkeiten
- Schlussfolgerung
Wenn wir die Güte eines Forecast-Modells evaluieren, müssen wir die Erwartungswerte betrachten, die es generiert. Dies geschieht durch die Berechnung geeigneter Fehlermaße (auch Fehlermetriken). Mit Hilfe von Fehlermetriken ist es möglich, die Güte eines Modells zu quantifizieren. Sie bieten Datenexperten somit eine Möglichkeit, verschiedene Modelle quantitativ zu vergleichen. Mit ihnen ist es möglich, die Eignung von Modellen für bestimmte Aufgaben objektiv zu bewerten.
In diesem Beitrag finden Sie einige häufig verwendete Metriken für die Zeitreihenprognose. Wir klären, wie sie zu interpretieren sind und zeigen die Grenzen der einzelnen Fehlermaße auf. Eine kleine Warnung vorweg: Um ein bisschen Mathematik kommen wir dabei nicht herum. Sie ist notwendig, um zu erklären, wie diese Metriken funktionieren. Für alle, die lieber auf Gleichungen verzichten, haben wir Interpretation und Einschränkungen deutlich gekennzeichnet. Springen Sie einfach zu diesem Abschnitt für eine Erklärung ohne Begriffe aus der Mathematik.
Mittlerer absoluter Fehler (MAE)
Der Mean Absolute Error, kurz MAE, ist definiert als der Durchschnitt der absoluten Differenz zwischen prognostizierten Werten und wahren Werten.
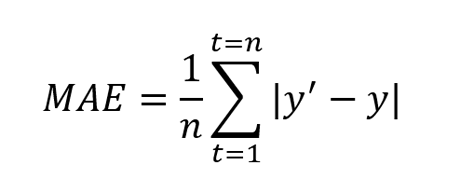
Dabei ist y’ der prognostizierte Wert und y der wahre Wert. n ist die Gesamtzahl der Werte in der Testmenge. MAE sagt uns, wie groß der Fehler ist, den wir im Durchschnitt vom Forecast erwarten können. Die Fehlerwerte sind in den ursprünglichen Einheiten der prognostizierten Werte und ein MAE von 0 bedeutet, dass kein Fehler in den prognostizierten Werten vorliegt.
Je niedriger der MAE-Wert ist, desto besser ist das Modell; ein Wert von Null bedeutet, dass kein Fehler im Forecast vorliegt. Wenn Sie also mehrere Modelle vergleichen, ist das Modell mit dem niedrigsten MAE-Wert das zu bevorzugende.
MAE eignet sich jedoch nicht für Informationen über die relative Größe des Fehlers. Deshalb ist es schwierig, große Fehler von kleinen Fehlern zu unterscheiden. In Kombination mit anderen Metriken lässt sich auch die relative Größe feststellen (siehe Root Mean Square Error unten). Außerdem kann MAE Probleme überdecken, die mit geringem Datenvolumen zu tun haben; siehe die letzten beiden Metriken in diesem Artikel, die sich für dieses Problem eignen.
Mittlerer absoluter prozentualer Fehler (MAPE)
Der Mean Absolute Percentage Error, kurz MAPE, ist definiert als der prozentuale Mittelwert der absoluten Differenz zwischen prognostizierten Werten und wahren Werten, geteilt durch den wahren Wert.
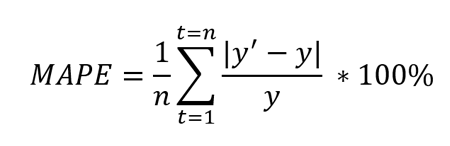
Dabei ist y’ der prognostizierte Wert und y der wahre Wert. n ist die Gesamtzahl der Werte in der Testmenge. Wegen des y im Nenner eignen sich Daten ohne Null- und Extremwerte am besten. Wenn dieser y-Wert extrem klein oder groß ist, nimmt auch der MAPE-Wert einen Extremwert an.
Je niedriger der MAPE-Wert, desto besser ist das Modell. Beachten Sie, dass MAPE am besten mit Daten ohne Null- und Extremwerte funktioniert. Wie MAE unterschätzt auch MAPE die Auswirkungen von großen, aber seltenen Fehlern aufgrund von Extremwerten. Um dieses Problem zu umgehen, kann der mittlere quadratische Fehler (Mean Squared Error) verwendet werden. Auch diese Metrik kann Probleme überdecken, die mit geringem Datenvolumen zu tun haben; siehe die letzten beiden Metriken in diesem Artikel, um diese Schwäche auszugleichen.
Mittlerer quadratischer Fehler (MSE)
Der Mean Squared Error, kurz MSE, ist definiert als der erwartete quadratische Abstand des Schätzwerts. Er wird auch als die Metrik definiert, die die Qualität des Prognosemodells oder Prädiktors bewertet. MSE beinhaltet sowohl die Varianz (die Streuung der vorhergesagten Werte zueinander) als auch die Verzerrung (der Abstand des vorhergesagten Wertes von seinem wahren Wert).
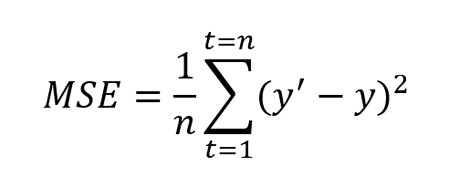
Dabei ist y’ der prognostizierte Wert und y ist der wahre Wert. n ist die Gesamtzahl der Werte im Testsatz. MSE ist fast immer positiv und Werte näher an Null sind besser. Aufgrund des quadratischen Terms (wie in der obigen Formel zu sehen), bestraft diese Metrik große Fehler oder Ausreißer mehr als kleine Fehler.
Je näher an Null der MSE ist, desto besser. Er löst zwar das Extremwert- und Null-Problem von MAE und MAPE, kann aber in einigen Fällen nachteilig sein. Diese Metrik kann Probleme übersehen, wenn es um geringe Datenmengen geht. Der Gewichtete absolute prozentuale Fehler und gewichtete mittlere absolute prozentuale Fehler bieten hier Lösungswege.
Wurzel des mittleren quadratischen Fehlers (RMSE)
Der Root Mean Squared Error, kurz RMSE, ist eine Erweiterung von MSE und ist definiert als die Quadratwurzel des mittleren quadratischen Fehlers.
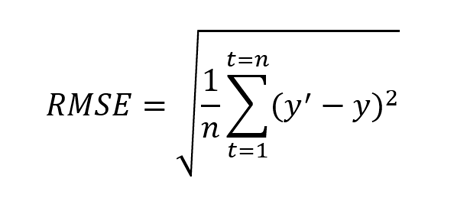
Dabei ist y’ der prognostizierte Wert und y der wahre Wert. n ist die Gesamtzahl der Werte in der Testmenge. Wie MSE, bestraft auch diese Metrik größere Fehler stärker.
Auch diese Metrik ist immer positiv und kleinere Werte sind besser. Ein Vorteil dieser Berechnung ist, dass der RMSE-Wert in der gleichen Einheit wie der prognostizierte Wert ist. Dadurch ist er im Vergleich zum MSE leichter zu verstehen.
RMSE kann auch mit MAE verglichen werden, um festzustellen, ob ein Forecast große, aber seltene Fehler enthält. Je größer die Differenz zwischen RMSE und MAE ist, desto inkonsistenter ist die Fehlergröße. Diese Metrik kann Probleme überdecken, die mit geringem Datenvolumen zu tun haben; siehe die letzten beiden Metriken in diesem Beitrag, um dieses Problem zu behandeln.
Wurzel des mittleren quadratischen Fehlers, normalisiert (NRMSE)
Der Normalized Root Mean Squared Error, kurz NRMSE, ist eine Erweiterung von RMSE und wird durch Normalisierung von RMSE berechnet. Es gibt zwei gängige Methoden zur Normalisierung des RMSE: Verwendung des Mittelwerts oder Verwendung des Bereichs der wahren Werte (Differenz von Minimal- und Maximalwert).
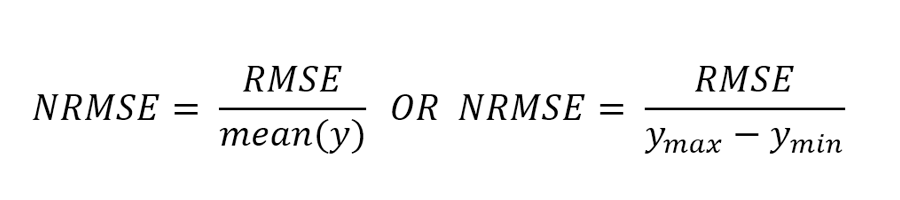
Dabei ist ymax der maximale wahre Wert und ymin der minimale wahre Wert.
NRMSE wird oft verwendet, um verschiedene Datensätze oder Prognosemodelle zu vergleichen, die unterschiedliche Skalen haben (z. B. Einheiten und Bruttoumsatz). Je kleiner der Wert ist, desto besser ist die Leistung des Modells. Diese Metrik kann Probleme übersehen, wenn die Datenmenge klein ist; siehe gewichteter absoluter prozentualer Fehler und gewichteter mittlerer absoluter prozentualer Fehler, um dem entgegenzuwirken.
Gewichteter absoluter prozentualer Fehler (WAPE)
Der Weighted Average Percentage Error, kurz WAPE, ist definiert als der gewichtete Durchschnitt des mittleren absoluten Fehlers.
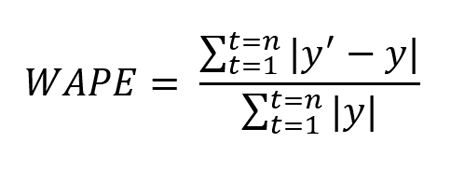
Dabei ist y’ der prognostizierte Wert und y der wahre Wert. n ist die Gesamtzahl der Werte in der Testmenge.
Die oben erwähnten Fehlermetriken helfen uns, die Leistung des Forecasting-Modells zu messen, können aber trügerisch sein, wenn nur geringe Datenmengen zur Verfügung stehen. Beispielsweise wenn der wahre Wert einiger Datenpunkte im Vergleich zum Rest der Daten sehr klein ist (etwa bei intermittierenden Nachfrage-/Verkaufsdaten). Für solche Fälle eignet sich der WAPE.
Je niedriger der Wert des WAPE ist, desto besser ist die Leistung des Modells. Durch die Gewichtung hilft der WAPE, kleinere von größeren Fehlern zu unterscheiden. Diese Metrik verhindert also, dass die kleinen Werte als gleichwertig oder höher in die Rechnung einfließen als größere Werte.
Gewichteter mittlerer absoluter prozentualer Fehler (WMAPE)
Der Weighted Mean Absolute Percentage Error, kurz WMAPE, ist eine Erweiterung von WAPE und wird als gewichteter mittlerer absoluter Prozentfehler definiert.
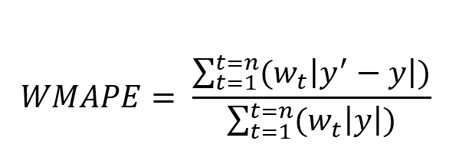
Dabei ist y’ der prognostizierte Wert und y der wahre Wert. n ist die Gesamtzahl der Werte in der Testmenge.
Je niedriger der Wert von WMAPE ist, desto besser ist die Leistung des Modells. Diese Metrik ist hilfreich für Daten mit geringem Volumen, bei denen jede Beobachtung eine andere Priorität bei der Bewertung von Vorhersagemodellen hat. Beobachtungen mit höherer Priorität haben einen höheren Gewichtungswert. Je größer der Fehler bei Prognosewerten mit hoher Priorität ist, desto größer ist der WMAPE-Wert.
Spannbreite von Fehlern und Ungenauigkeiten
Bei Verwendung der oben genannten Fehlermetriken ist die tatsächliche Verteilung der Fehlerwerte nicht bekannt. Diese Verteilung kann jedoch weitere Einblicke in das Verhalten des Forecasting-Modells geben und bei der Auswahl der am besten geeigneten Metrik helfen. Im Jedox AIssisted™ Planning Wizard wird neben den oben genannten Metriken auch die Fehlerverteilung berechnet, d. h. der Wert der Metrik für jeden Datenpunkt des Testsatzes. Eine Zusammenfassung der Verteilung, die auch andere relevante Werte wie den minimalen, maximalen und medianen Fehlerwert enthält, wird ebenfalls bereitgestellt.
Schlussfolgerung
Die Vielzahl der Metriken macht die Wahl nicht unbedingt leichter. Jede Metrik liefert spezifische Informationen, die, je nach Anwendungsfall, mehr oder minder geeignet sind. Daher sollte eine Metrik auf der Grundlage des Anwendungsfalls und des Verständnisses der Daten, die für die Forecasts benötigt werden, ausgewählt werden.
Übersicht der Fehlermetriken für Forecasts
- MAE ist nützlich, wenn es um darum geht, den absoluten Fehler zu messen. Sie ist einfach zu verstehen, aber nicht effizient, wenn die Daten Extremwerte aufweisen.
- MAPE ist ebenfalls leicht zu verstehen und wird verwendet, wenn es darum geht, verschiedene Forecasting-Modelle oder Datensätze zu vergleichen. Der Prozentwert eignet sich dafür besonders. MAPE hat aber den gleichen Nachteil wie MAE: Die Metrik ist nicht effizient, wenn die Daten Extremwerte aufweisen.
- MSE ist nützlich, wenn die Streuung der Forecastwerte wichtig ist und größere Werte normalisiert werden müssen. Allerdings ist diese Metrik oft schwer zu interpretieren, da es sich um einen quadrierten Wert handelt.
- RMSE (NRMSE) ist ebenfalls nützlich, wenn die Streuung von Bedeutung ist und Extremwerte normalisiert werden müssen. RMSE ist im Vergleich zu MSE leichter zu interpretieren, da der RMSE-Wert die gleiche Skala wie die prognostizierten Werte hat.
- WAPE ist nützlich, wenn nicht viele Daten vorliegen, da eine Gewichtung anhand aller wahren Werte stattfindet.
- WMAPE ist ebenfalls nützlich, wenn es sich um wenige Daten handelt. WMAPE hilft dabei, die Priorität zu berücksichtigen, indem das Gewicht (Prioritätswert) jeder Beobachtung verwendet wird.
Jedox bietet eine umfassende Übersicht über Vorhersagefehler und deren Verteilung im AIssisted™ Planning Wizard, genauso wie einen unvoreingenommener Blick in die Zukunft mit Predictive Forecasting.